Examples¶

Simple state machine
Complex hierarchical state machine
Different ways to attach event handlers
Reverse Polish notation calculator

Simple state machine ¶

This is a simple state machine with only two states - on and off.

from pysm import State, StateMachine, Event

on = State('on')
off = State('off')

sm = StateMachine('sm')
sm.add_state(on, initial=True)
sm.add_state(off)

sm.add_transition(on, off, events=['off'])
sm.add_transition(off, on, events=['on'])

sm.initialize()

def test():
    assert sm.state == on
    sm.dispatch(Event('off'))
    assert sm.state == off
    sm.dispatch(Event('on'))
    assert sm.state == on


if __name__ == '__main__':
    test()

Complex hierarchical state machine ¶

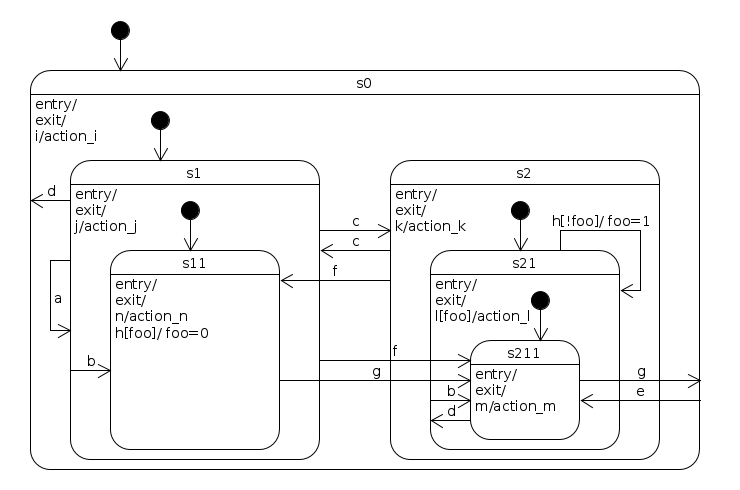
A Hierarchical state machine similar to the one from Miro Samek’s book [1], page 95. It is a state machine that contains all possible state transition topologies up to four levels of state nesting [2]

from pysm import State, StateMachine, Event

foo = True

def on_enter(state, event):
    print('enter state {0}'.format(state.name))

def on_exit(state, event):
    print('exit state {0}'.format(state.name))

def set_foo(state, event):
    global foo
    print('set foo')
    foo = True

def unset_foo(state, event):
    global foo
    print('unset foo')
    foo = False

def action_i(state, event):
    print('action_i')

def action_j(state, event):
    print('action_j')

def action_k(state, event):
    print('action_k')

def action_l(state, event):
    print('action_l')

def action_m(state, event):
    print('action_m')

def action_n(state, event):
    print('action_n')

def is_foo(state, event):
    return foo is True

def is_not_foo(state, event):
    return foo is False


m = StateMachine('m')
s0 = StateMachine('s0')
s1 = StateMachine('s1')
s2 = StateMachine('s2')
s11 = State('s11')
s21 = StateMachine('s21')
s211 = State('s211')

m.add_state(s0, initial=True)
s0.add_state(s1, initial=True)
s0.add_state(s2)
s1.add_state(s11, initial=True)
s2.add_state(s21, initial=True)
s21.add_state(s211, initial=True)

# Internal transitions
m.add_transition(s0, None, events='i', action=action_i)
s0.add_transition(s1, None, events='j', action=action_j)
s0.add_transition(s2, None, events='k', action=action_k)
s1.add_transition(s11, None, events='h', condition=is_foo, action=unset_foo)
s1.add_transition(s11, None, events='n', action=action_n)
s21.add_transition(s211, None, events='m', action=action_m)
s2.add_transition(s21, None, events='l', condition=is_foo, action=action_l)

# External transition
m.add_transition(s0, s211, events='e')
s0.add_transition(s1, s0, events='d')
s0.add_transition(s1, s11, events='b')
s0.add_transition(s1, s1, events='a')
s0.add_transition(s1, s211, events='f')
s0.add_transition(s1, s2, events='c')
s0.add_transition(s2, s11, events='f')
s0.add_transition(s2, s1, events='c')
s1.add_transition(s11, s211, events='g')
s21.add_transition(s211, s0, events='g')
s21.add_transition(s211, s21, events='d')
s2.add_transition(s21, s211, events='b')
s2.add_transition(s21, s21, events='h', condition=is_not_foo, action=set_foo)

# Attach enter/exit handlers
states = [m, s0, s1, s11, s2, s21, s211]
for state in states:
    state.handlers = {'enter': on_enter, 'exit': on_exit}

m.initialize()


def test():
    assert m.leaf_state == s11
    m.dispatch(Event('a'))
    assert m.leaf_state == s11
    # This transition toggles state between s11 and s211
    m.dispatch(Event('c'))
    assert m.leaf_state == s211
    m.dispatch(Event('b'))
    assert m.leaf_state == s211
    m.dispatch(Event('i'))
    assert m.leaf_state == s211
    m.dispatch(Event('c'))
    assert m.leaf_state == s11
    assert foo is True
    m.dispatch(Event('h'))
    assert foo is False
    assert m.leaf_state == s11
    # Do nothing if foo is False
    m.dispatch(Event('h'))
    assert m.leaf_state == s11
    # This transition toggles state between s11 and s211
    m.dispatch(Event('c'))
    assert m.leaf_state == s211
    assert foo is False
    m.dispatch(Event('h'))
    assert foo is True
    assert m.leaf_state == s211
    m.dispatch(Event('h'))
    assert m.leaf_state == s211


if __name__ == '__main__':
    test()

Different ways to attach event handlers ¶

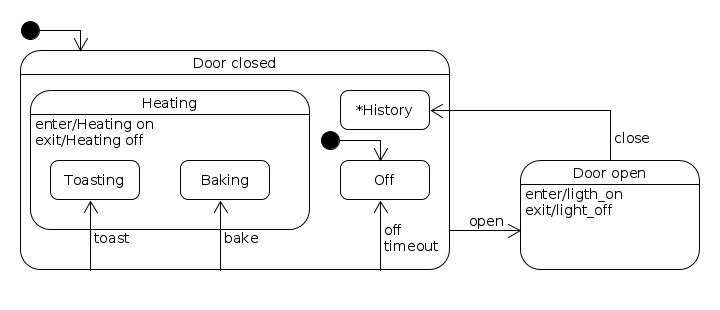
A state machine and states may be created in many ways. The code below mixes many styles to demonstrate it (In production code you’d rather keep your code style consistent). One way is to subclass the State class and attach event handlers to it. This resembles the State Pattern way of writing a state machine. But handlers may live anywhere, really, and you can attach them however you want. You’re free to chose your own style of writing state machines with pysm. Also in this example a transition to a historical state is used.

import threading
import time
from pysm import StateMachine, State, Event


# It's possible to encapsulate all state related behaviour in a state class.
class HeatingState(StateMachine):
    def on_enter(self, state, event):
        oven = event.cargo['source_event'].cargo['oven']
        if not oven.timer.is_alive():
            oven.start_timer()
        print('Heating on')

    def on_exit(self, state, event):
        print('Heating off')

    def register_handlers(self):
        self.handlers = {
            'enter': self.on_enter,
            'exit': self.on_exit,
        }


class Oven(object):
    TIMEOUT = 0.1

    def __init__(self):
        self.sm = self._get_state_machine()
        self.timer = threading.Timer(Oven.TIMEOUT, self.on_timeout)

    def _get_state_machine(self):
        oven = StateMachine('Oven')
        door_closed = StateMachine('Door closed')
        door_open = State('Door open')
        heating = HeatingState('Heating')
        toasting = State('Toasting')
        baking = State('Baking')
        off = State('Off')

        oven.add_state(door_closed, initial=True)
        oven.add_state(door_open)
        door_closed.add_state(off, initial=True)
        door_closed.add_state(heating)
        heating.add_state(baking, initial=True)
        heating.add_state(toasting)

        oven.add_transition(door_closed, toasting, events=['toast'])
        oven.add_transition(door_closed, baking, events=['bake'])
        oven.add_transition(door_closed, off, events=['off', 'timeout'])
        oven.add_transition(door_closed, door_open, events=['open'])

        # This time, a state behaviour is handled by Oven's methods.
        door_open.handlers = {
            'enter': self.on_open_enter,
            'exit': self.on_open_exit,
            'close': self.on_door_close
        }

        oven.initialize()
        return oven

    @property
    def state(self):
        return self.sm.leaf_state.name

    def light_on(self):
        print('Light on')

    def light_off(self):
        print('Light off')

    def start_timer(self):
        self.timer.start()

    def bake(self):
        self.sm.dispatch(Event('bake', oven=self))

    def toast(self):
        self.sm.dispatch(Event('toast', oven=self))

    def open_door(self):
        self.sm.dispatch(Event('open', oven=self))

    def close_door(self):
        self.sm.dispatch(Event('close', oven=self))

    def on_timeout(self):
        print('Timeout...')
        self.sm.dispatch(Event('timeout', oven=self))
        self.timer = threading.Timer(Oven.TIMEOUT, self.on_timeout)

    def on_open_enter(self, state, event):
        print('Opening door')
        self.light_on()

    def on_open_exit(self, state, event):
        print('Closing door')
        self.light_off()

    def on_door_close(self, state, event):
        # Transition to a history state
        self.sm.set_previous_leaf_state(event)


def test_oven():
    oven = Oven()
    print(oven.state)
    assert oven.state == 'Off'
    oven.bake()
    print(oven.state)
    assert oven.state == 'Baking'
    oven.open_door()
    print(oven.state)
    assert oven.state == 'Door open'
    oven.close_door()
    print(oven.state)
    assert oven.state == 'Baking'
    time.sleep(0.2)
    print(oven.state)
    assert oven.state == 'Off'


if __name__ == '__main__':
    test_oven()

Reverse Polish notation calculator ¶

A state machine is used in the Reverse Polish notation (RPN) calculator as a parser. A single event name (parse) is used along with specific inputs (See pysm.pysm.StateMachine.add_transition()).

This example also demonstrates how to use the stack of a state machine, so it behaves as a Pushdown Automaton (PDA)

import string as py_string
from pysm import StateMachine, Event, State


class Calculator(object):
    def __init__(self):
        self.sm = self.get_state_machine()
        self.result = None

    def get_state_machine(self):
        sm = StateMachine('sm')
        initial = State('Initial')
        number = State('BuildingNumber')
        sm.add_state(initial, initial=True)
        sm.add_state(number)
        sm.add_transition(initial, number,
                          events=['parse'], input=py_string.digits,
                          action=self.start_building_number)
        sm.add_transition(number, None,
                          events=['parse'], input=py_string.digits,
                          action=self.build_number)
        sm.add_transition(number, initial,
                          events=['parse'], input=py_string.whitespace)
        sm.add_transition(initial, None,
                          events=['parse'], input='+-*/',
                          action=self.do_operation)
        sm.add_transition(initial, None,
                          events=['parse'], input='=',
                          action=self.do_equal)
        sm.initialize()
        return sm

    def parse(self, string):
        for char in string:
            self.sm.dispatch(Event('parse', input=char))

    def calculate(self, string):
        self.parse(string)
        return self.result

    def start_building_number(self, state, event):
        digit = event.input
        self.sm.stack.push(int(digit))
        return True

    def build_number(self, state, event):
        digit = event.input
        number = str(self.sm.stack.pop())
        number += digit
        self.sm.stack.push(int(number))
        return True

    def do_operation(self, state, event):
        operation = event.input
        y = self.sm.stack.pop()
        x = self.sm.stack.pop()
        # eval is evil
        result = eval('float({0}) {1} float({2})'.format(x, operation, y))
        self.sm.stack.push(result)
        return True

    def do_equal(self, state, event):
        operation = event.input
        number = self.sm.stack.pop()
        self.result = number
        return True


def test_calc_callbacks():
    calc = Calculator()
    assert calc.calculate(' 167 3 2 2 * * * 1 - =') == 2003
    assert calc.calculate('    167 3 2 2 * * * 1 - 2 / =') == 1001.5
    assert calc.calculate('    3   5 6 +  * =') == 33
    assert calc.calculate('        3    4       +     =') == 7
    assert calc.calculate('2 4 / 5 6 - * =') == -0.5

if __name__ == '__main__':
    test_calc_callbacks()

Footnotes

[1]	Miro Samek, Practical Statecharts in C/C++, CMP Books 2002.

[2]	http://www.embedded.com/print/4008251 (visited on 07.06.2016)

Examples¶

Simple state machine¶

Complex hierarchical state machine¶

Different ways to attach event handlers¶

Reverse Polish notation calculator¶

Simple state machine ¶

Complex hierarchical state machine ¶

Different ways to attach event handlers ¶

Reverse Polish notation calculator ¶